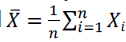필기용 블로그

○Computing Expectations by conditioning

 ▷Condition을 걸어서 기대값을 구해야 하는 경우

 ▷재귀적인 문제 (선택 이후 선택이 처음과 같음)를 푸는데 유용함.

 ◎앞면이 나올때까지 동전 던지기 (Geomatric)

  ▷Condition Y -> 1: 첫 던지기가 앞면 / 0:첫 던지기가 뒷면

  ▷Y가 0이면, 1회를 추가한 뒤, 다시 동전을 던지는 것 (E[N])과 같다.

 ◎Quick Sort Average Comparison

  ▶Quicksort

   ▷pivot 선택

   ▷leftmark, rightmark가 순회하며 pivot과 비교. (left가 pivot보다 크고, right가 pivot보다 작으면 멈추고, 둘 다 멈춰있으면 서로 바꾼다.)

   ▷leftmark, rightmark가 서로 같은 위치거나 교차하면, pivot과 바꾼다.

   ▷pivot기준 left partition, right partition에 대해 반복한다.

  ▶Expectation of comparison

   ▷Mn -> E[N], Condition j -> pivot이 j번째로 작은 수

○Computing Variances by conditioning

 ▷Condition을 걸어서 분산을 구해야 하는 경우

 ▷Computing Expectation by condition을 이용한다.

 ◎Gemmatric random variale (확률 p)

  ▷E[N] = 1/p

  ▷Condition Y -> 1: 처음이 성공 / 0: 처음이 실패

  ▷E[N^2|Y=0] = E[(N+1)^2] = E[N^2] + 2E[N] + 1

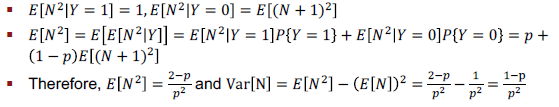
○Computing Probabilities by conditioning

 ▷Condition을 걸어서 확률을 걸어야 하는 경우

 ▷각 조건에서 확률들의 합을 구한다.

 ◎사고가 일어날 횟수(n)에 대한 확률

  ▷사고 빈도가 λ일때, 내년에 사고가 n번 일어날 확률 - Poisson(λ)

  ▷사고 빈도 λ - Exp(λ)

  ▷Gamma Random Variable의 PDF를 이용

 ◎Ballet Problem

  ▷선거에서, 출마자 A(n표 받음)와 B(m표 받음)가 있을 때, 개표 방송에서 A가 항상 이길 확률 = (n-m)/(n+m) 임을 증명

  ▷P_n,m = A가 마지막 표를 받았을때, A가 항상 이길확률 × A가 마지막에 표를 받았을 확률 + B가 마지막 표를 받았을때, A가 항상 이길확률 × B가 마지막에 표를 받았을 확률

  ▶수학적 귀납법 (P_n,m = (n-m)/(n+m)에 대해서

   ▷총 개표수가 1일때, 성립한다. 

   ▷총 개표수가 n+m-1 = k인것들에 대해 성립한다면

   ▷총 개표수가 n+m인 것에 대해서도 성립한다. 

○Conditional PMF (discrete case)

 ▷조건부 확률에 대한 PMF (Y가 y일때, X에 대한 확률)

 ▷E[X|Y = y] = Σ x×( p_X|Y(x|y) )

 ▶Binomial: X_1 = Binomial (n_1, p) / X_2 = Binomial (n_2, p)

  ▷X_1, X_2가 독립일 때

 ▶Poisson: X_1 = Poisson(λ_1) / X_2 = Poisson(λ_1)

  ▷X_1, X_2가 독립일 때

○Conditional PMF (continuous case)

 ▷조건부 확률에 대한 PMF (Y가 y일때, X에 대한 확률)

 ▷E[X|Y = y] = ∫ x×( f_X|Y(x|y) ) 

●Covariance (공분산)

 ▷2개의 확률변수의 상관 정도를 나타내는 값

 ▷Cov(X, Y) = E[XY] - E[X]E[Y]

 ▷X, Y가 독립이면, Cov(X, Y) = 0

 ▶속성

  ▷Cov(X, X) = Var(X)

  ▷Cob(X, Y) = Cov(Y, X)

  ▷Cov(aX, bY) = ab×Cov(X, Y)

  ▷Cov(X, Y+Z) = Cov(X, Y) + Cov(X, Z)

  ▷

  ▶만약 X_1~X_i가 서로 독립이고 동일한 distribution을 가질 때 (E[X_i] = μ / Var(X_i) = σ^2)

   ▷값을 아래와 같이 정의하면

   ▷다음과 같은 성질을 가진다.

●Joint Distribution Function (결합 확률 분포)

 ▷2개 이상의 Random Variable 에 대한 확률 분포

○Joint Cumulative Distribution Function (Joint CDF)

 ▷Continus한 두 Random variable X, Y에 대해 다음과 같이 정의함.

 ▷두 조건 (X ≤ a, Y ≤ b)을 모두 만족하는 경우를 고려

 ▶속성

  ▷F_X,Y( -∞,-∞ ) = F_X,Y( -∞,y ) = F_X,Y( x,-∞ ) = 0

  ▷F_X,Y( ∞,∞ ) = 1

  ▷0 ≤ F_X,Y( x,y ) ≤ 1

  ▷F_X,Y( x,∞ ) = F_X(x) / F_X,Y( ∞,y ) = F_Y(y)

  ▷F_X,Y( x_1 ≤ X ≤x_2, y_1 ≤ Y ≤y_2 ) = F_X,Y(x_2, y_2) - F(x_1, y_2) - F(x_2, y_1) + F(x_1, y_1) ≥ 0

 ▶Expectation

  ▷값 구하는 방법 (ex) X+Y)을 이용해서 값×확률을 적분한다.

○Joint Probability Mass Function (Joint PMF)

 ▷discrete한 두 Random variable X, Y에 대해 다음과 같이 정의함.

 ▷두 조건 (X = a, Y = b)을 모두 만족하는 경우를 고려

 ▶Expectation

  ▷X -> E(X) / Y -> E(Y) (ex) E[X+Y] = E(X) + E(Y))

  ▷E(XY) ≠ E(X)E(Y)에 주의.

   ▷X, Y가 Independent (서로의 결과에 영향X)인 경우에는 E(XY) ＝ E(X)E(Y)이다.

※Convolution (합성곱)

 ▷X, Y가 독립이고 X, Y의 pdf가 각각 f, g일때 P(X+Y)에 대한 CDF, PDF

○Variance

 ▷분산

 ▷데이터가 평균에 대해 얼마나 퍼져있는지.

 ▷(관측값 - 평균)^2 / 개수

 ▷Var(X) = E[X^2] - (E[X])^2