●Graphs
▶Graph G = (V, E)
▷V : Set of Vertex(Nodes), 정점 - Vertices
▷E : Collection of pairs of Vertices - Edges
▷V, E는 positions이고, elements를 저장한다.
▶종류
▶Directed graph
▷모든 edge가 Directed edge - 순서가 정해진 Edge (Origin(tail) -> Destination(head) )

▶Undirected graph
▷모든 edge가 Undirected edge - 순서가 없는 Edge

▶활용
▷전기회로
▷교통망
▷컴퓨터 네트워크
▷데이터베이스
▶용어

▶Endpoints of an edge
▷edge에 연결된 두 vertices
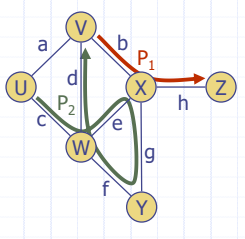
▷a - U, V
▶Edges incident on a Vertex
▷vertex에 연결된 edges
▷V - a, d, b
▶Adjacent vertices (인접한 vertices)
▷edge 하나로 연결되는 vertices
▷U, V
▶Degree of a vertex
▷vertex에 연결된 edges의 개수 (loop - 2개처리)
▷X : 5
▶Parallel edges
▷동일한 vertices와 연결된 edges
▷h, i
▶Self-loop (loop)
▷하나의 vertex와 연결된 edge
▷j
▶Path
▷하나의 Vertex로부터 edges, vertices를 거쳐 다른 Vertex로 가는 길
▶Simple Path
▷거치는 모든 Vertices, Edges가 반복되지 않음

▶Cycle
▷시작 Vertex와 끝 Vertex가 동일한 Path
▶Simple Cycle
▷거치는 모든 Vertices, Edges가 반복되지 않음
▶Subgraph
▷한 Graph의 일부로 만든 다른 Graph
▷Subgraph G' = (V', E')에서 V' ⊆ V, E' ⊆E
▶Spanning subgraph
▷Graph의 모든 Vertex는 포함하지만, 일부 Edge를 포함하지 않음.
▷Spanning subgraph G' = (V', E')에서 V' = V, E' ⊆E
▶Connected Graph
▷모든 Vertex pair에 대해 한쪽에서 다른 한쪽으로 가는 path가 존재함.
▶Connected component
▷가능한 최대로 연결된 connected subgraph
▶Complete Graph
▷모든 Vertex에 대해 가능한 최대의 edge를 연결한 것.
▷edge 개수 : v(v-1)/2 (v: vertex 개수)
▶(Free) Tree
▷Cycle이 없는 Undirected Connected Graph
▷Spanning Tree : Tree인 Spanning subgraph
▶Forest
▷Cycle이 없는 Undirected Graph
▷Forest의 Connected components는 Tree이다.
▷Spanning Forest : Forest인 Spanning subgraph
▶속성 (v : vertex 개수, e : edge 개수)
▷Σdeg(v) = 2e
▷e ≤ v(v-1)/2 - complete graph의 edge 개수보다 작거나 같다.
○Graph ADT
▷Vertices, Edges는 position으로 구현한다.
▷element를 저장한다.
▶메소드
▶Accessor
▷e.endVertices() : e의 Endpoint vertices의 list 반환
▷e.opposite(v) : e에서 v의 반대쪽에 있는 vertex 반환
▷u.isAdjacentTo(v) : u와 v가 adjacent하다면 true 반환
▷*v : vertex v의 element
▷*e : edge e의 element
▶Update
▷insertVertex(o) : element o를 저장하는 vertex를 생성
▷insertEdge(v, w, o) : v, w vertices를 연결하는 element o 를 저장하는 edge 생성
▷eraseVertex(v) : vertex v 제거
▷eraseEdge(e) : edge e 제거
▶iterable collection
▷incidentEdges(v) : v와 연결된 edges의 list
▷vertices() : 그래프의 모든 vertices의 list
▷edges() : 그래프의 모든 edges의 list
▶Edge List Structure

▶Vertex Object
▷element를 저장
▷vertex sequence에서 position을 저장
▶Edge Object
▷element를 저장
▷edge sequence에서 position을 저장
▷origin/destination vertex object를 저장
▶Vertex sequence : vertex objects의 sequence
▶Edge sequence : edge objects의 sequence
▷Vertex에 관한 메소드가 비효율적
▶Adjacency List Structure

▷Edge List Structure를 기반으로 함.
▷Vertex 메소드의 효율성 개선
▶각 Vertex에 Incidence sequence 추가
▷각 Vertex가 Incident edges의 List를 가짐.
▶각 Edge가 Incidence sequece에서 자신의 position을 저장
▶Adjacency Matrix Structure

▷Edge List Structure를 기반으로 함.
▷각 Vertex가 고유한 Integer key값을 가지고 있음.
▶2차원 배열 Adjacency array
▷행의 Key값, 열의 Key값이 연결되는 Edge를 가졌다면, 그 Edge에 reference함. (Nondirected - 대각선에 대해 대칭)
▷연결되는 edge가 없으면 null값
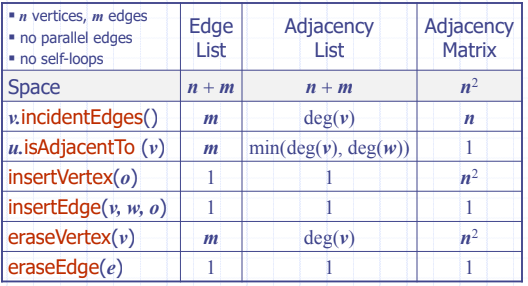
▶Performance
'컴퓨터 지식 > 자료구조' 카테고리의 다른 글
| Graph Traversal (0) | 2020.12.10 |
|---|---|
| Heap (0) | 2020.12.05 |
| Priority Queues (0) | 2020.12.04 |
| Binary Tree (0) | 2020.11.20 |
| Tree (0) | 2020.11.20 |