○Binary Tree
▶다음 규칙들을 가진 Tree
▷각 노드가 최대 2 개의 자식 노드를 가진다.
▷노드의 자식은 ordered pair를 이룬다. (left child, right child의 순서가 다르면 다른 Tree)
▶재귀적 정의
▷single node로 이루어져 있거나
▷root가 ordered pair인 자식을 지니고, 각각이 binary tree이다.
▶ADT
▷Tree ADT의 확장
▶Additional methods
▷position p.left(): left child의 position
▷postion p.right(): right child의 position
▶예시
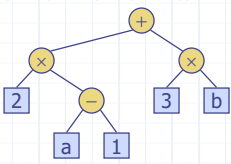
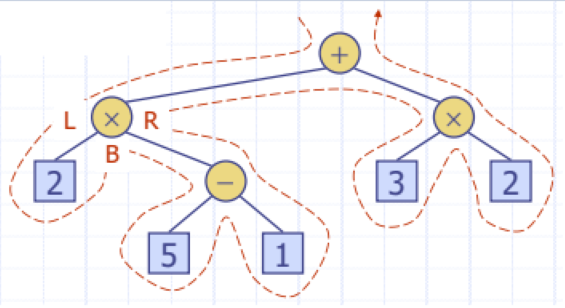
▶Arithmetic Expression Tree: 수학 계산을 나타내는 Tree
▷Internal nodes: 연산자
▷External nodes: 피연산자
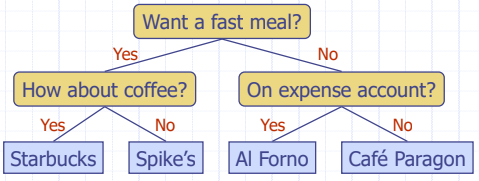
▶Decision Tree: yes/no 결정을 나타내는 Tree
▷Internal nodes: yes/no의 답을 할 수 있는 질문
▷External nodes: 결정(결론)
▶Proper Binary Tree
▷자식 노드가 0개 또는 2개이다. (1개일 경우 없음)
▶성질 (n: 노드 수 / e: external node 수 / i: internal node 수 / h: height)
▷e = i + 1
▷n = 2e - 1
▷h ≤ i
▷h ≤ (n-1/2
▷e ≤ 2h
▷h ≥ log2e
▷h ≥ log2(n+1) - 1
▶순회
▶Inorder Traversal
▷left child -> node -> right child 순으로 순회
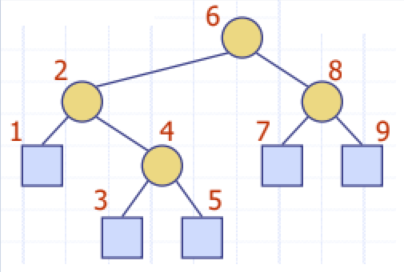
▷Artithmetic Expressions를 출력할 때 사용 가능
▷left subtree이전에 (, right subtree이후에 )추가

▶Postorder traversal
▷Arithmetic Expressions를 계산할 때 사용가능
▷양 옆의 노드를 재귀호출 (External -> 값, Internal -> 계산한 값)

▶Euler Tour Traversal
▷일반적인 Binary Tree 순회방법
▷Tree를 왼쪽에서부터 따라 가며, 노드들을 방문함. (한 노드당 최대 3번 방문 가능)
▷Proper binary tree인 경우, internal node에 대해서는 반드시 3회 방문한다. (external - 1회)
▶구현
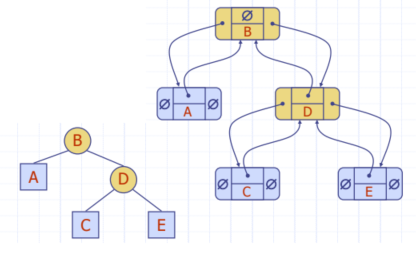
▶Linked Structure
▷Position ADT를 포함한다.
▷각 노드는 다음의 정보를 가진다.
▷Element (요소)
▷Parent node
▷Left Child
▷Right Child
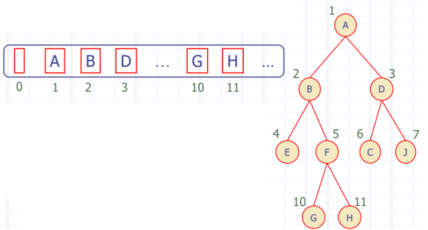
▶Array-Based Representation
▷Node들은 Array[rank(v)]에 저장되어있다.
▷각 child에는 다음과 같이 저장되어있다.
▷left child: rank(node) = 2×rank(parent(node)]
▷right child: rank(node) = 2×rank(parent(node)]+1
'컴퓨터 지식 > 자료구조' 카테고리의 다른 글
| Heap (0) | 2020.12.05 |
|---|---|
| Priority Queues (0) | 2020.12.04 |
| Tree (0) | 2020.11.20 |
| Sequence (0) | 2020.11.20 |
| Iterator, Container (0) | 2020.11.06 |