●Group
▷nonempty set G와 binary operation □에 대해
▷<G, □>이 다음을 만족하면 Group이다.
▶조건 - <G, □>
▷Closure under □: a,b ∈ G에서 a □ b ∈ G
▷Associative: a, b, c ∈ G에서 (a □ b) □ c = a □ (b □ c).
▷Existence of an Identity: e ∈ G에서 e □ a = a □ e = a
▷Existence of Inverses: 각각 a ∈ G에 대해 a ́ □ a = a □ a ́ = e인 a' ∈ G가 존재한다.
▷abelian 조건 - Commutative: a,b ∈ G에서 a □ b = b □ a
▶Order of Group ( |G| )
▷Group element의 개수
▷유한하지 않다면 무한하다.
▶성질
▷identity(항등원)은 유일하다.
▷각 element에 대해 inverse(역원)은 유일하다.
▷a, b, c ∈ G에서 ab = ac가 성립하면, b = c이다. (Left-cancellation) (a □ b = ab)
▷a, b, c ∈ G에서 ba = ca가 성립하면, b = c이다. (Right-cancellation) (a □ b = ab)
○Subgroup
▷G의 부분집합 H (H ⊆ G)에 대해
▷H가 binary operation □를 만족하는 group이다.
▷{e-identity}와 G(자기 자신)는 모든 Group에 대해 Subgraph이다.
▶조건
▷Closure under □: a,b ∈ H에서 a □ b ∈ H
▷Existence of Inverses: 각각 a ∈ H에 대해 a ́ □ a = a □ a ́ = e인 a' ∈ H가 존재한다.
▷위의 두 조건을 만족하면, 나머지 조건들도 만족한다.
▷G의 nonempty finite subset H에 대해, H가 □에대해 closed하면, H는 G의 Subgroup이다. (<->)

○Direct Product ( <G×H, ◇> )
▷<G , □>,<H, △> 가 Group일때
▷G×H에서 연산자 ◇를 다음과 같이 정의하면
▷(g1, h1) ◇ (g2, h2) = (g1 □ g2, h1 △ h2)
▷<G×H, ◇> 는 G와 H의 Direct Product이다.
○Power of Elements (a^n)
▷(a □ b = ab라고 할때
▷a^0 = e
▷a^1 = a
▷a^n = a^(n-1) a
▷a^(-n) = (a^-1)^n
▷a^m a^n = a^(m+n)
▷(a^m)^n
○Homomorphism
▷<G , □>,<H, △> 가 Group이고, f : G -> H일때
▷모든 a, b에 대해 a, b ∈ G, f (a □ b) = f (a) △ f (b)이면
▷f는 group homorphism이다.
▶속성
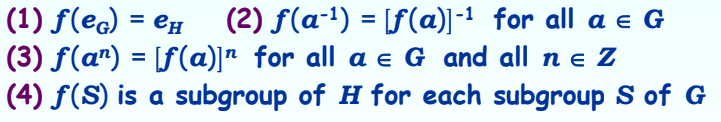
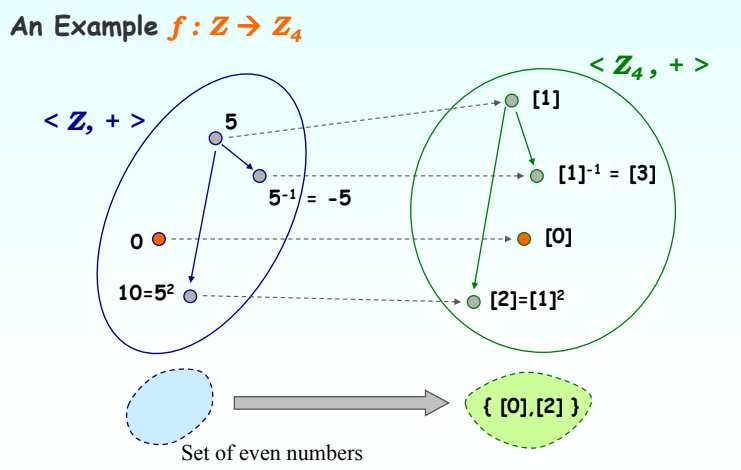
▶Isomorphism
▷f: <G , □> -> <H, △>이 homomorphism일때
▷one-to-one(1대1 대응), onto(공격 = 치역) 관계를 만족하면
▷G, H는 isomorphic groups이다.
'수학 > 이산수학' 카테고리의 다른 글
| Euler Theorem ... (0) | 2020.11.04 |
|---|---|
| Cyclic Group (0) | 2020.10.29 |
| Euclidean Algorithm (0) | 2020.10.25 |
| Modular Arithmetic (0) | 2020.10.25 |
| Algebra (0) | 2020.10.24 |