필기용 블로그

●Assembly Code

 ▷Machine Code를 텍스트로 나타낸 것.

 ▷gcc -Og -S 파일명

 ▶자료형

  ▷int: 1, 2, 4, 8 bytes (정확하지 않음)

  ▷float: 4, 8, 10 bytes (정확하지 않음)

  ▷Array, Structure같은 여러 개가 한번에 묶인 타입은 없음

○연산

 ▷Register / 메모리 데이터에 대해 산술 연산

 ▷data load / store 가능

 ▶레지스터

  ▷정수, 메모리 주소 ... 등을 저장

  ▷피연산자, 연산의 결과를 저장하는 공간.\

  ▷%rax : 8바이트 / %eax : 4바이트 / 2바이트, 1바이트로 끊어서도 사용 가능 -> 호환 가능하도록

 ▶피연산자 (Operand)

  ▷상수: $0x400 과 같이 $를 이용해 구분

  ▷레지스터: %rax, ...

  ▷메모리 주소: (%rax), 메모리 주소로 접근? (*의 역할?)

 ▶메모리 접근

  ▷C에서의 배열과 유사 (Ri: 인덱스, S: 원소 크기)

 ▶연산자 (Operator)

  ▷크기에 따라 사용하는 연산자가 다름. (q: 8바이트, l: 4, w:2, b:1)

  ▷대부분 Source, Destination의 순서를 가짐.

  ▶종류

   ▷mov[q]: Destination에 Source를 저장. 대입 연산자와 유사

   ▷lea[q]: Memory reference를 하지 않고 (*를 하지 않고), 주소를 계산. x+k*y를 계산하는데 주로 사용

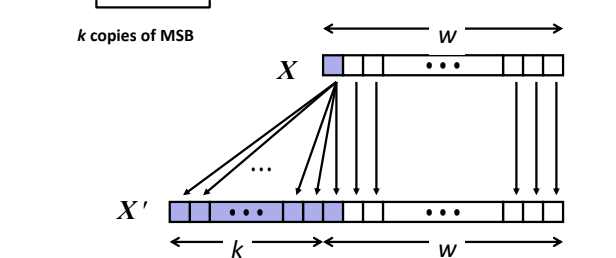
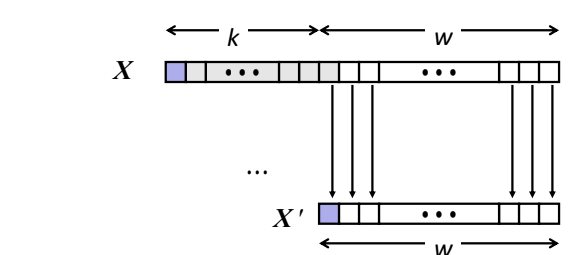
   ▶Zero Extension (movz[b][l])

    ▷작은 단위에서 큰 단위로 값을 확장한다. (b(1)<w(2)<l(4)<q(8)) 남는 공간은 0으로 채운다.

●Architecture

 ▷컴퓨터 시스템의 하드웨어 구조

 ▷Processor design의 일부로써, machine / assembly code를 쓰기 위해 이해할 필요가 있음

 ▷ISA (Instruction Set Architecture): 마이크로프로세서가 인식해서 기능을 이해하고 실행할 수 있는 기계어 명령어

 ▷Microprocessor: 초소형 연산장치, CPU

 ▶C -> Object Code

○Object Code

 ▷Assembly의 각 명령어를 binary Code로 변환

 ▷다른 파일과 linkage가 빠져있음. -> Linker가 해결

 ▶Disassembling

  ▷objdump -d 오브젝파일 > 파일명 / Vi 파일명

  ▷gdb sum / (gdb) disassemble 파일/함수명 

●Float (실수)

 ▷컴퓨터로 실수를 표현하는 방법

 ▶바이트 크기

  ▷float: 4

  ▷double: 8

 ▶2진수의 소수 표현 (기본)

  ▷특정 위치를 소수점의 기준으로, 2^n의 합을 계산함.

  ▷10진수의 모든 수를 2진수로 표현할 수 없음 (순환소수)

  ▷비트의 범위를 넘어가는 아주 작은 값이나 아주 큰 값을 나타낼 수 없음 (범위가 작음)

 ▶Floating Point Representation

  ▶(-1)^s × M × 2^E

   ▷s: Sign bit, 부호를 나타냄

   ▷M: Significand, 소수점 이하 부분을 나타냄 (1.xxxxx), frac값을 이용해 계산

   ▷E: Expoennt, 2의 지수를 나타냄. exp값을 이용해 계산.

  ▶바이트 크기 (s-frac-exp)

   ▷float(32): 1-8-23

   ▷double(64): 1-11-52

   ▷extended(80): 1-15-63/64

  ▶exp값에 따른 종류

   ▶Normaized Value: exp ≠ 0000... / 1111...

    ▷E= exp - Bias(=2^(k-1)-1) -> 범위는 -(2^(k-1) -2) ≤ E ≤ 2^(k-1) -1

    ▷M은 1로 시작한다는 전제로, frac을 선언. (1.xxxxxx 에서 xxxxx이 frac) -> 범위는 1.0 ≤ M ＜ 2.0 - ε

   ▶Demormalized Value: exp = 0000...

    ▷E = 1-Bias = -(2^(k-1)-2)

    ▷M = 0.xxxx -> 0과 그에 가까운 값들을 표현

   ▶Special Value: exp = 1111...

    ▷frac = 0000... -> 무한대, Sign값에 따라 +∞ / -∞ 가 결정

    ▷frac ≠ 0000.... -> Not a Number (NaN)

 ▶Float Comparison

  ▷부호 비트 비교

  ▷-0 = 0임을 주의

  ▷NaN값 고려 (어떻게 처리할것인가)

  ▷나머지는 Unsigned Int와 비슷하게 비교 가능

 ▶Float Operation

  ▶Rounding (값을 정확히 표현가능하지 않을경우, 유사한 값으로 맞춤)

   ▷toward zero (0과 가까운 값)

   ▷round down (내림)

   ▷round up (올림)

   ▷nearest even (짝수 우선-기본): 반올림을 기본으로 5인경우, 짝수쪽으로 올림/내림

    ▷Postnormalize: Rounding 한 결과가 overflow를 일으키는 경우 (10.xxx)

     ▷exp를 1 더하고, fraction을 1.xxxx로 맞춤.

  ▶Multiplication

   ▷s : s1 ^ s2 (XOR)

   ▷M : M1 × M2

    ▷2를 넘으면 E를 1올리며 오른쪽으로 shift해야함

    ▷frac에 맞게 Round필요

   ▷E : E1 + E2

   ▷결합 법칙이 성립하지 않는다. (Overflow, Round 때문)

  ▶Addition

   ▷E: E1 (E1>E2 일때)

    ▷M2' = M2 × 2^(-E1+E2)

   ▷s: 결과에 맞춰서

   ▷M: 결과에 맞춰서, Round필요

   ▷결합 법칙이 성립하지 않는다. (Overflow, Round 때문)

●Integer (정수)

 ▷컴퓨터에서 정수를 표현하는 방법

 ▶바이트 크기

  ▷char: 1

  ▷short: 2

  ▷int: 4

  ▷long: 4 (32bit) / 8 (64bit)

 ▶음수 표현

  ▶부호 비트

   ▷가장 앞의 비트를 부호 비트로 지정한다. (앞이 1이면 -부호)

   ▷+0, -0이 동시에 존재한다.

   ▷+, - 연산이 힘들다.

  ▶1의 보수

   ▷해당 수에 대한 1의 보수(=모든 비트 반전)가 -부호.

   ▷+0, -0이 동시에 존재한다.

  ▶2의 보수

   ▷해당 수에 대한 2의 보수(2의 보수=1의 보수 +1)가 -부호.

   ▷0도 하나이고, +/- 연산도 잘 되기 때문에, 가장 선호된다.

   ▷앞으로 나오는 모든 음수는 2의 보수로 계산하는 것을 전제로 한다.

 ▶Type Casting

  ▶Signed <-> Unsigned

   ▷둘 모두 0111->1000을 제외하고는 비트가 커질수록 커진다.

   ▷비트 패턴이 유지되며, 암시적일 경우에는 Signed가 Unsigned로 Casting된다.

  ▶int -> long (Expanding)

   ▷부호비트 확장

  ▶long -> int (Truncating)

   ▷앞의 k-bits 자르기. -> 정보 손실 가능성

 ▶Operation

  ▶Addition

   ▷두 비트를 더하고, 표현 가능 범위를 넘어가면 자름.

   ▷Unsigned의 경우 Overflow가 하나, Signed는 두개(Pos, Neg) 존재함.

  ▶Multiplication

   ▷Unsigned: 범위를 넘어가는 상위 비트 무시

   ▷Signed: 범위를 넘어가는 상위 비트 무시

   ▶Shift 연산 이용 (2의 지수승 이용)

    ▷u << k = u * 2^k임을 이용하여, Shift연산, Addition연산으로 Multiplication 계산

  ▶Divide (Shift 이용)

   ▷u >> k = u / 2^k임을 이용.

   ▷0 이하에서는 내림이 반대로 되기 때문에, 약간의 수정이 필요

   ▷(x+2^k -1) / 2^k [ x+(1<<k)-1) >> k ]

  ▶Negation (-부호)

   ▷~x + 1 = - x

   ▷x가 TMin이거나 0일때는, x = -x

●Bit

 ▷0 또는 1을 가지는 2진수값 (0: 꺼짐 (ex) 0V 근처) / 1: 켜짐 (ex) 1V 근처))

 ▷여러 개의 bits를 해석하는 방법에 따라 다른 정보를 의미하게 됨.

 ▶Byte

 ▷1byte = 8bits

 ▷10진수: 0~255 / 16진수: 00~FF

○Boolean Algebra (부울 연산)

 ▷And [A&B]: 둘 다 1이면 1

 ▷Or [A|B]: 둘 중 하나가 1이면 1

 ▷Xor (Exclusive Or) [A^B]: 둘이 다르면 1

 ▷Not [~A]: 1이면 0, 0이면 1

 ▷Left Shift [A<<n]: n만큼 왼쪽으로 시프트 (비트를 민다.), 오른쪽은 0으로 채운다

 ▷Right Shift [A>>n]: n만큼 오른쪽으로 시프트 (비트를 민다.)

  ▷logical shift: 0으로 채움

  ▷arithmetic shift: 부호 비트 (최상위 비트)로 채움

 ▶Byte Ordering

  ▷Big Endian: 상위 비트가 앞에 (01 23 45 67)

  ▷Little Endian: 하위 비트가 앞에 (67 45 23 01)