○비교를 위한 함수들
▷Constant: 1
▷Logarithmic: log(n)
▷Linear: n
▷N-Log-N: n log(n)
▷Quadratic: n^2
▷Cubic: n^3
▷Exponential: 2^n
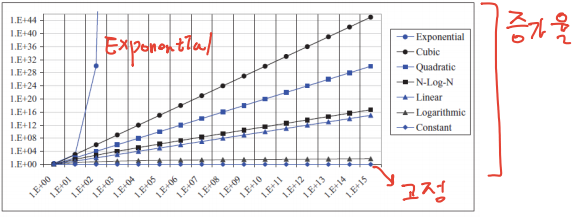
○실행 시간 비교
▷평균을 잡는 것은 힘들기 때문에, 최악의 경우를 고려함.
▷같은 조건하게 구현하여 시간을 측정하는 것은, 구현이 필요하며 특정 Input을 고려하지 못하고 하드웨어/소프트웨어가 동일해야함.
▷RAM 접근과 계산에 일정한 시간을 가진다고 고려. -> Operation 개수로 시간을 비교
▶성장도
▷Input값이 증가함에 따라 시간이 어떻게 변하는지.
▷주로 함수들로 표현함.
▷상수, 하위의 차수에 영향받지 않음 (-> 무시가능)
▶Big-Oh Notation (O(g(n))
▷n ≥ n_0일때, f(n) ≤ cg(n) 일때, f(n)은 O(g(n)) 이라고 한다. (f(n) is Big-Oh of g(n))
▷n_0보다 클 때, 항상 cg(n) 보다 작거나 같다. (최악의 경우)
▷성장률이 g(n)보다 작거나 같다, g(n)은 주로 위의 함수들로 표현한다. (상수 -> c로 가기 때문에 무시 가능)
▶Big-Omega (Ω(g(n))
▷n_0보다 클 때, 항상 cg(n) 보다 크거나 같다.
▶Big-Theta (Θ(g(n))
▷n_0보다 클 때, 항상 cg(n)과 같다.
※Pseudo Code
