● Linear Independence
▷v_1 ... v_n의 벡터들에 대해
c_1×v_1 + c_2×v_2 + ... c_n×v_n = 0
이 성립하는 경우는 모든 c가 0인 경우를 제외하곤 존재하지 않는다.
▶Linearly independent 한 경우
▷Linearly independent한 set의 subset인 경우
● Linear dependence
▷v_1 ... v_n의 벡터들에 대해
c_1×v_1 + c_2×v_2 + ... c_n×v_n = 0
이 성립하는데 몇몇 c가 0이 아닌 경우가 존재한다.
▶Linearly dependent 한 경우
▷A = [v_1 v_2 ... v_n] 이 singular 하다.
▷Subset S가 오직 0벡터로만 구성되어있다.
▷Subset S의 원소 v_1 ... v_n 중 최소 하나의 벡터가 다른 벡터들의 선형 조합(또는 한 벡터의 스칼라곱)으로 이루어져 있다.
▷0벡터를 포함하는 벡터의 집합이다.
▷Linearly dependent한 set을 포함하는 set인 경우
▶Wronskian function
▷f_1, f_2 ... f_n ∈ F(R) 에서 아래와 같은 행렬식의 값.
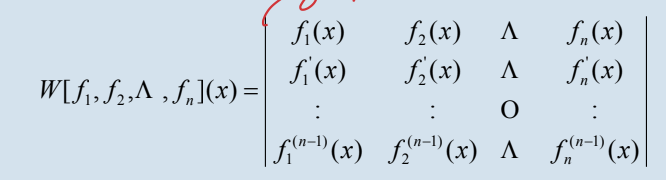
▷W( f_1, f_2 ... f_n )(x_0) != 0 인 x_0( ∈R )가 존재한다면 f_1, f_2 ... f_n는 lineary independent 하다.
'수학 > 공학선형대수학' 카테고리의 다른 글
| Vector Space (0) | 2020.06.22 |
|---|---|
| Adjoint of Matrix (0) | 2020.06.21 |
| 행렬식 (Determinant) (0) | 2020.06.21 |
| Elementary Matrix, LU Factorization (0) | 2020.06.20 |
| 행렬(Matrix) 기초 (0) | 2020.06.19 |